Information-Theoretic Bayesian Optimization of Imaging Systems

Leyla A. Kabuli, Nalini M. Singh, Henry Pinkard, Laura Waller
Department of Electrical Engineering and Computer Sciences,
University of California, Berkeley
Correspondence to: lakabuli@berkeley.edu

Optica Imaging Congress (COSI) 2025
Extended Abstract

Abstract

We present a black-box imaging system design framework using Bayesian optimization and mutual information. Our approach, as demonstrated in lensless imaging and radio astronomy, does not require a forward encoding model, ground truth data, or image reconstruction.

Overview

Computational imaging systems capture measurements with a hardware encoder and recover images with a computational decoder. An open question in computational imaging is optimal encoder design. For example, phase mask designs for compressive encoding in lensless imaging must take into account object-dependent performance, and telescope positions for radio astronomy must be carefully selected, as telescopes are costly to build.

In this work, we provide a method for automatic black-box encoder design. In contrast with end-to-end design, which requires a differentiable encoding model and joint optimization with a reconstruction algorithm, our approach uses Bayesian optimization to treat the imaging system as a black box, and directly evaluates system measurements using mutual information, which quantifies the amount of information the measurement captures about objects of interest.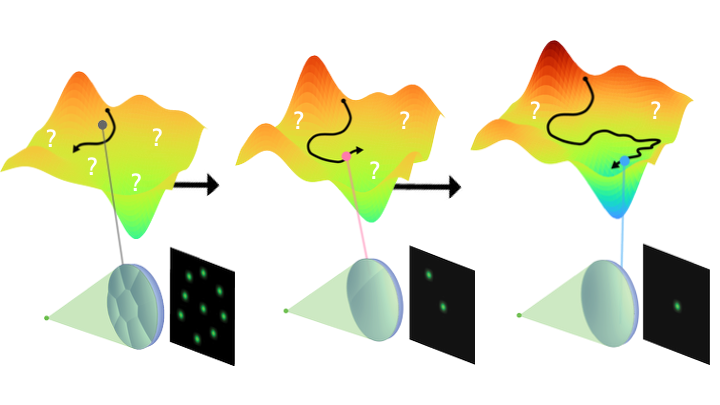
Bayesian optimization steps


Applications

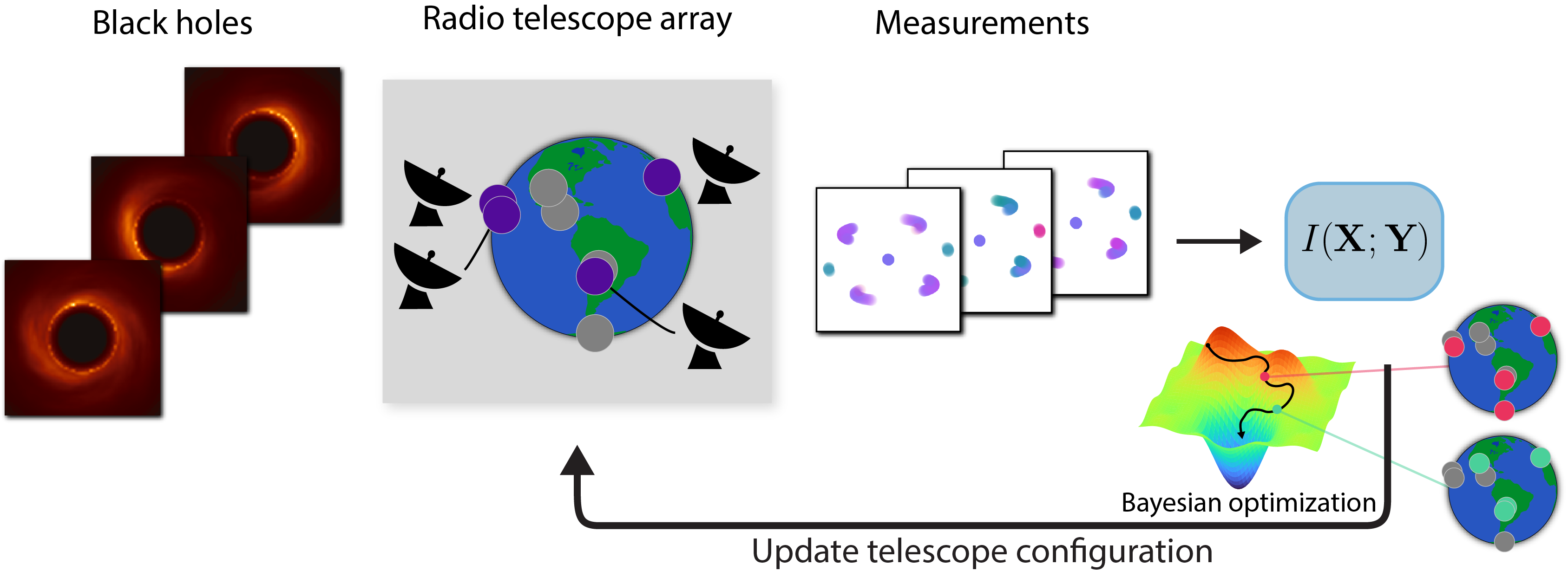
We demonstrate two examples of design using our method: phase mask design for a lensless imaging system and a radio telescope array design for black hole imaging in radio astronomy.

We first validate our approach by optimizing the positions and numbers of lenslets for a phase mask with the goal of maximizing encoded information when imaging natural objects.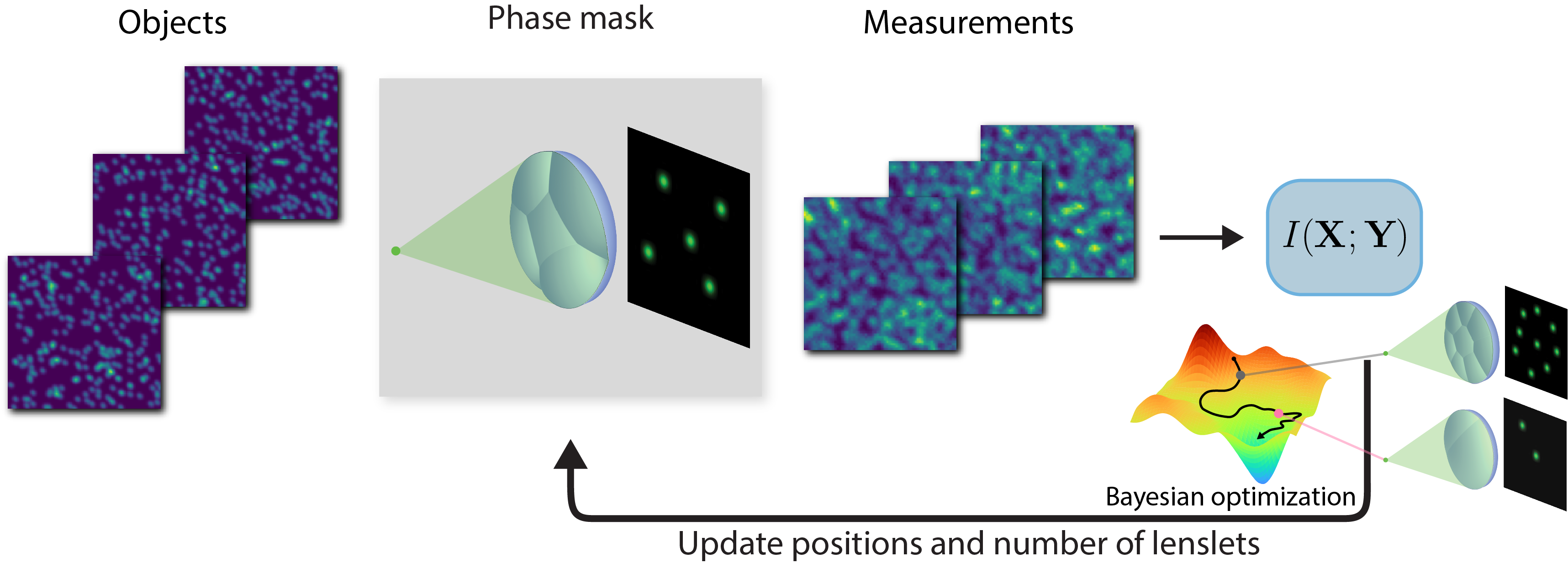
Lensless imaging design process
As visualized below, we confirm that a single lens system is optimal for imaging natural objects in 2D. We then optimize a phase mask for compressive lensless imaging of sparse objects. As visualized below, we find that a five lenslet phase mask is optimal in this case. Next, we optimize a telescope array for black hole imaging in radio astronomy. In this problem, our parameters are telescope locations, which are chosen from a set of valid positions. This combinatorial problem has a discrete search space, which is well-suited for our black-box approach. In constrat, standard differentiable design approaches, such as end-to-end design, cannot be used for this sort of parameter space.
Radio astronomy design process
As visualized below, we find the optimal set of four telescopes given eight candidate positions using our black-box information-driven design approach.

Next Steps

Our design framework generalizes to many other computational imaging scenarios and we are actively looking for new applications and collaborations for our work.

Related Links

Also check out our work on Information-driven design of imaging systems, our work on Designing lensless imaging systems to maximize information capture, and our work on Estimation-theoretic methods for lensless imaging system analysis.

BibTeX

@inproceedings{kabuli2025blackboxinfo,
  author    = {Kabuli, Leyla A. and Singh, Nalini M. and Pinkard, Henry and Waller, Laura},
  title     = {Information-Theoretic Bayesian Optimization of Imaging Systems},
  booktitle = {Optica Imaging Congress (3D, COSI, DH, FLatOptics, IS, pcAOP)},
  journal   = {Optica Imaging Congress (3D, COSI, DH, FLatOptics, IS, pcAOP)},
  publisher = {Optica Publishing Group},
  pages = {Paper CTu1B.4},
  year      = {2025}  
}